السرداب ما لا يخطر على بال
درجة كثيرات الحدود
كثيرات الحدود هي دوال رياضية مكونة من متغيرات وأعداد ثابتة مرتبطة بعلامات الجمع والطرح والضرب. وتُعرف درجة كثير الحدود بأنها أعلى أس لمتغير في كثير الحدود.
الأساسيات
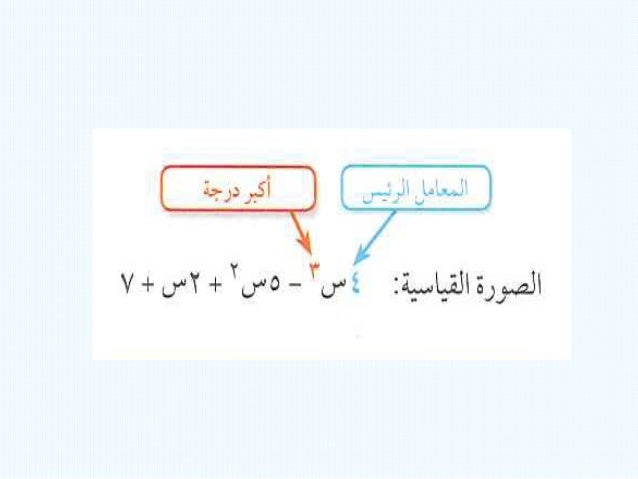
كثير الحدود من الدرجة الأولى يُسمى خطيًا، وكثير الحدود من الدرجة الثانية يُسمى تربيعيًا، وكثير الحدود من الدرجة الثالثة يُسمى تكعيبيًا.
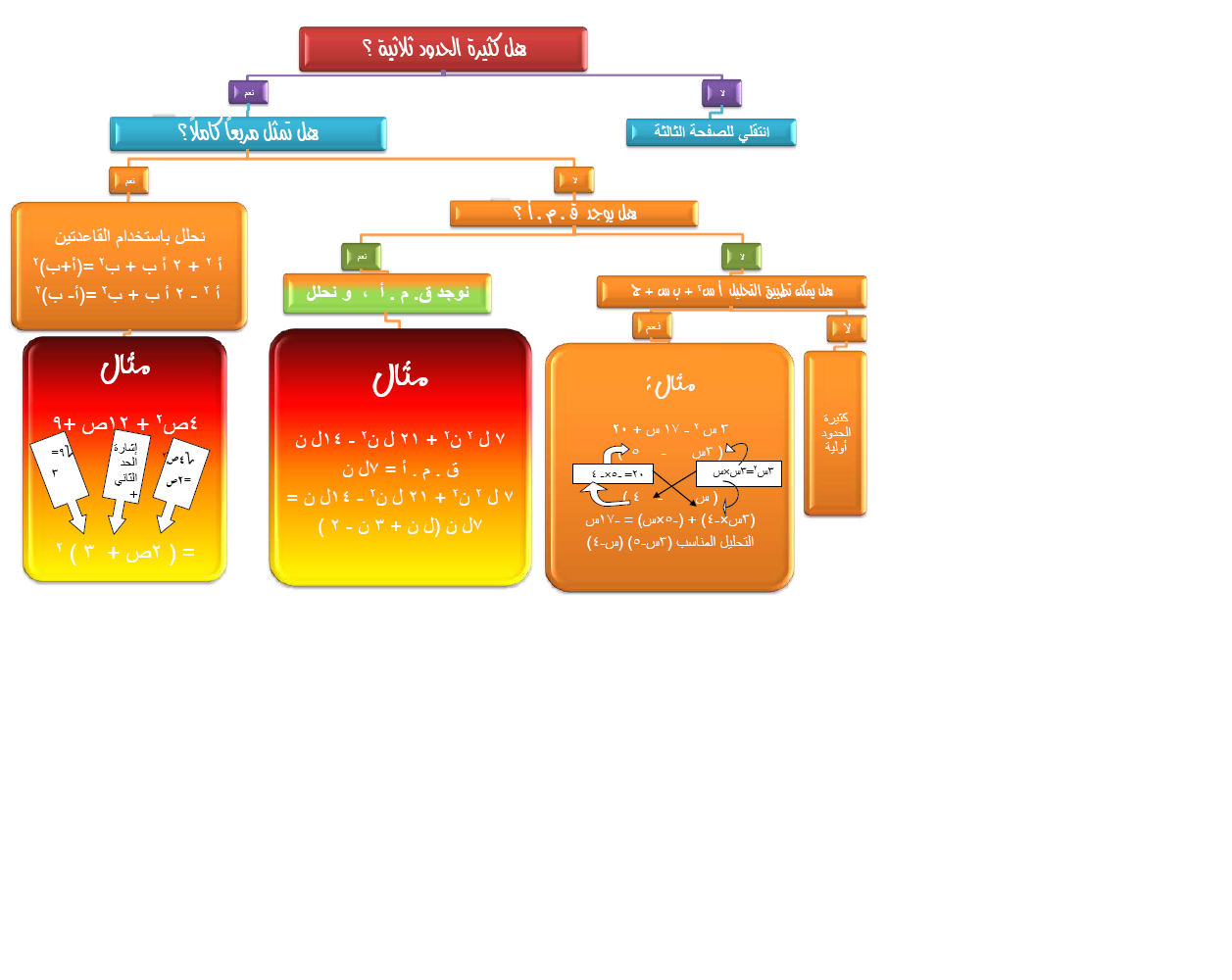
تُستخدم درجات كثيرات الحدود في العديد من التطبيقات، مثل حساب التكامل والتفاضل وإيجاد جذور كثيرات الحدود.
أنواع كثيرات الحدود
هناك أنواع مختلفة من كثيرات الحدود، بما في ذلك:
- كثيرات الحدود الأحادية: تحتوي على متغير واحد فقط.
- كثيرات الحدود المتعددة المتغيرات: تحتوي على أكثر من متغير واحد.
- كثيرات الحدود المتجانسة: تحتوي على متغيرات لها نفس الدرجة.
- كثيرات الحدود غير المتجانسة: تحتوي على متغيرات بدرجات مختلفة.
عمليات كثيرات الحدود
يمكن إجراء العديد من العمليات على كثيرات الحدود، بما في ذلك:
- الجمع والطرح: يمكن الجمع أو طرح كثيرتي حدود بنفس الدرجة عن طريق إضافة أو طرح معاملات المتغيرات المتشابهة.
- الضرب: يمكن ضرب كثيرات الحدود باستخدام طريقة فويل أو طريقة الضرب العمودي.
- القسمة: يمكن قسمة كثير الحدود على كثير حدود آخر لإيجاد ناتج وباقي.
جذور كثيرات الحدود
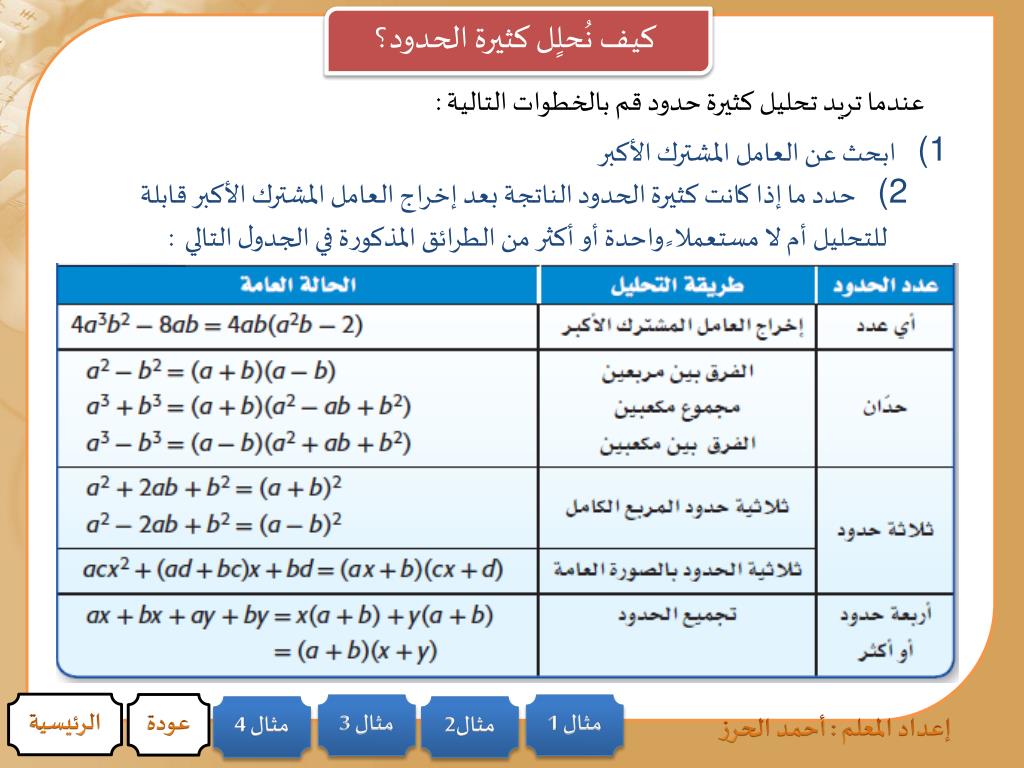
يُطلق على قيم المتغيرات التي تجعل كثير الحدود يساوي صفرًا جذور كثير الحدود.
يمكن إيجاد جذور كثيرات الحدود من الدرجة الأولى والثانية باستخدام الصيغ التربيعية.
لتحديد جذور كثيرات الحدود من الدرجات العليا، يمكن استخدام طرق مثل طريقة نيوتن رافسون أو طريقة التقسيم الاصطناعي.
تطبيقات كثيرات الحدود
لكثيرات الحدود العديد من التطبيقات في الرياضيات والهندسة والعلوم.
تُستخدم كثيرات الحدود في:
- حساب المساحات والحجوم.
- إيجاد نقاط التقاطع بين المنحنيات.
- نمذجة الظواهر الفيزيائية مثل الحركة والديناميكا.
استنتاج
درجة كثير الحدود هي مفهوم أساسي في الجبر وتُستخدم في العديد من التطبيقات. من خلال فهم درجة كثير الحدود وأنواعها وعملياتها وجذورها وتطبيقاتها، يمكننا استخدام كثيرات الحدود لحل مجموعة واسعة من المشكلات الرياضية والعلمية.
